Payasos Matemágicos

Hoy os traemos un juego de matemagia muy interesante, basado en un principio con muchas posibilidades. Para hacerlo, necesitaréis unas cartas especiales que podéis descargar en el siguiente enlace:

Una vez que tengas el documento debes imprimirlo a doble cara. Es importante que te fijes bien en que en la parte trasera de cara tarjeta debe aparecer el mismo payaso que en la parte delantera, pero dividido en 4 partes. Si en la delantera el sombrero es rojo, el pelo azul…, en la trasera deben aparecer exactamente las mismas piezas, sombrero rojo, pelo azul, etc. Si las cartas no te han quedado así, posiblemente no has girado el papel de forma correcta para imprimir en la otra cara. Las cartas están diseñadas para ser recortadas por el lado en el que aparecen los payasos divididos en partes. En el otro lado quedarán unas orlas blancas que permiten que el corte sea preciso aunque la impresión a doble cara no esté perfectamente alineada.

Para explicar las instrucciones sobre cómo se lleva a cabo el juego lo mejor es que veáis el siguiente vídeo en el que se explica todo el proceso.

 

¿Cómo funciona?

Como ves la secuencia de pasos para hacer el efecto es sencilla:

• El espectador piensa en uno de los payasos, es necesario recordar el número y los colores de alguno de los elementos de su ropa.
• En los siguientes pasos todo sucederá mostrando siempre la cara de las cartas que tiene los payasos completos, sin darles la vuelta.
• Primero hay que colocar los payasos en un montón, en orden numérico (es indiferente si quedan ordenados del 1 al 8 o del 8 al 1).
• Se reparten uno a uno los payasos en dos montones, y tras una pregunta colocamos siempre el montón que NO tiene el payaso del espectador encima del que sí lo tiene. En lugar de preguntar directamente al espectador en qué montón está su payaso puedes intentar adivinarlo, e ir improvisando el guión según aciertes o falles en tu adivinación. Lo importante en cualquier caso es dejar el montón que NO tiene el payaso elegido sobre el que si lo tiene
• Repite el paso anterior dos veces más, haciendo un total de 3 repartos en dos montones, pero después del tercer reparto no montes el montón que no tiene el payaso encima del que sí lo tiene. En su lugar, si vas volviendo las cartas del montón que no tiene el payaso una a una, puedes construir, con las piezas que aparecen por detrás de la tarjeta, un nuevo payaso, que coincide en todos los colores con el payaso elegido por el espectador.
• Además, si retiras la primera carta del montón donde está el payaso elegido por el espectador, quedará a la vista el payaso elegido, que siempre queda al final del proceso en la segunda posición de ese montón.

¿Por qué funciona?

Como siempre explicamos en nuestros cursos y conferencias, una de las cosas más bellas de la matemagia es que el hecho de saber cómo funciona aún sigue siendo mágico y fascinante, porque sigue quedando la pregunta de ¿por qué funciona? Para explicarlo en este caso, vamos a tener que contar unos cuantos conceptos de magia matemática.

La idea original de este efecto surge del estudio del juego “Con ocho cartas”, que aparece en la página 32 del libro “Magia por principios” del genial matemago y amigo Pedro Alegría. Puedes conseguir este libro pulsando aquí.

La mezcla faro

El funcionamiento de este juego de matemagia tiene que ver, en primer lugar con el concepto de mezcla faro. En pocas palabras hacer una mezcla faro sería cortar un montón exactamente por la mitad y hacer la clásica mezcla por “rifleo” de forma que quedasen las cartas intercaladas una a una. En rigor existen dos formas de hacer una mezcla faro en un montón con un número par de cartas.

Poniendo un ejemplo sencillo, en un montón de 8 cartas, 1-2-3-4-5-6-7-8, una mezcla faro out dejaría el montón con las primeras cuatro cartas intercaladas entre las últimas cuatro cartas, de forma que la primera carta se mantendría la primera y la última la última:

1-2-3-4-5-6-7-8  después de faro out quedaría 1-5-2-6-3-7-4-8.

La otra opción sería una mezcla faro in, en la que la primera carta pasaría a la segunda posición, quedando el montón de la siguiente forma:

1-2-3-4-5-6-7-8  después de faro in quedaría 5-1-6-2-7-3-8-4.

En este juego, no se utiliza la mezcla faro, sino más bien su proceso inverso, que llamamos mezcla antifaro. Repartir en dos montones las cartas, una a una, y colocar un montón encima de otro es el equivalente a “deshacer” una mezcla faro, por eso llamamos a este proceso mezcla antifaro. Además, que una vez repartido pongamos el montón en el que cayó la última carta encima del otro, o al revés, nos permitiría deshacer una mezcla faro in o una mezcla faro out, por tanto la decisión de poner el montón izquierdo encima del derecho o viceversa genera un cambio importante en el orden final del montón.

Hay una pequeña observación más: en realidad, dado que los payasos están todo el tiempo cara arriba, el hecho de repartir en dos montones no es una mezcla antifaro, porque se invierte además el orden de las cartas. De esta forma, si mi montón estuviese en el orden 1-5-2-6-3-7-4-8, después de repartir en dos montones y montar de la forma adecuada, no llegaría al orden 1-2-3-4-5-6-7-8, que sería hacer una antifaro out, sino al orden 8-7-6-5-4-3-2-1, con todas las cartas invertidas, puedes comprobarlo si quieres. Esto a nivel matemático es muy importante, pero las propiedades fundamentales del proceso se nos mantienen para el caso que estamos analizando.

Si tomo los payasos, hago el proceso de reparto, y monto un montón encima del otro, como tengo dos opciones para montar los montones, puedo llegar a dos ordenes finales: si el montón donde cae la última carta se monta encima del otro, la última carta terminará como primera; si monto de la otra forma, la última carta repartida quedará en posición 5ª desde arriba.

Al decidir después del reparto de que forma monto los dos montones, puedo hacer que la carta elegida por el espectador acabe en la posición final que yo elija. En nuestro caso, al montar siempre el montón que NO tiene el payaso elegido sobre el que sí, conseguiría, si monto también la tercera vez, que la carta elegida por el espectador termine en sexta posición.

Pero en realidad en cada uno de los tres repartos podría elegir si pongo encima el montón que tiene la carta elegida o el que no, de esa manera esas tres elecciones binarias me podrían llevar a ocho combinaciones de respuestas posibles, que son las 8 posiciones en las que podría terminar el payaso elegido por el espectador.

Por cierto, este patrón se mantendría si utilizamos 4 elecciones en un grupo de 16 cartas, 5 en un grupo de 32 y así sucesivamente.

La matriz de las diferentes permutaciones

Si llevo a cabo los tres repartos y estudio todas las posibles opciones a las que puedo llegar, en función de la decisión de que montón se coloca encima del otro, veo fácilmente que podré llegar a 8 ordenaciones diferentes, que se muestran en la siguiente imagen en forma de tabla. Cada columna representa una ordenación, de la parte superior a la inferior.

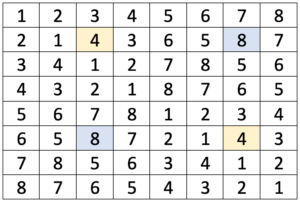
En esta tabla – matriz podemos observar una propiedad muy interesante: si tomo dos números iguales en cualquier parte de la matriz, puedo imaginarme que las posiciones que ocupan son vértices de un rectángulo. Si busco los otros dos vértices del rectángulo, puedo comprobar que serán también dos números iguales entre sí. En la imagen anterior se muestran dos 4 con fondo amarillo y dos 8 con fondo azul que ilustran dicha propiedad. Pero hay muchos más “rectángulos” que la cumplen, cualquiera que tenga vértices opuestos con el mismo valor tiene el otro par de vértices con el mismo valor. Matemáticamente diríamos que:

Esta propiedad nos genera un conjunto muy amplio de relaciones entre la posición inicial de las cartas y la posición final. Ya vimos anteriormente que el proceso del juego lleva el payaso elegido a la posición sexta, pero el hecho de empezar con un montón ordenado de payasos, que puedo diseñar a mi antojo, con la propiedad anterior, supondrá que puedo “emparejar” los payasos de diversas formas.

Si nos fijamos en cada columna de la matriz anterior, veremos que cuando el payaso 6 queda el 6º, el 1 queda el 1º, y cuando el 1 queda el 6º el payaso 6 queda el 1º. Esta es la propiedad que estamos describiendo de la matriz de permutaciones. Pero no pasa solo con el 1 y el 6, también quedan emparejados, para la relación entre posición primera y sexta, las parejas, 2-5, 3-8 y 4-7. Si diseñamos los payasos de forma que esas parejas tengan el mismo color de sombrero, pues al final del reparto habrá coincidencia de color entre las cartas que quedan en las posiciones correspondientes. De la misma forma podríamos emparejar los colores de pelo, camiseta… en realidad podríamos emparejar hasta 7 características de los personajes, aunque en este juego hemos utilizado solo 4  para que el desarrollo sea más rápido.

Al igual que dijimos antes, todas estas propiedades se mantienen para montones de 16 con 4 repartos, montones de 32 con 5 repartos y así sucesivamente.

Otras variantes

Hace tiempo publicamos un juego basado en el mismo principio. En ese caso hay alguna pequeña variación, porque las cartas sí se van volviendo cara arriba durante el reparto, por tanto son mezclas antifaros sin inversión. En aquella ocasión utilizamos para finalizar el juego la idea de los deletreos, de forma que a la hora de diseñar los gatitos tuvimos que estudiar en la matriz de permutaciones donde debía aparecer el gato correspondiente, ajustando el movimiento de cartas que nos daban los deletreos. Además en aquella ocasión en lugar de poner a la variable “sombrero” un valor de color, elegido entre 4 opciones, utilizamos un sistema de “¿pelaje blanco?” con respuesta solo binaria, sí o no. Echa un vistazo a la entrada correspondiente, es un juego muy interesante y en apariencia bastante distinto al de los payasos.

Gatitos matemágicos

Esperamos que nos compartáis vuestras ideas y diseños propios para seguir explorando este interesante principio matemágico.

¡¡¡Vivan las mates!!!