Una regla para dibujar espirales logarítmicas y deshacer mitos

¿Quién no ha escuchado alguna vez que la espiral áurea la podemos encontrar en la forma de la concha del nautilus? ¿Qué nos diríais si os demostráramos que esta afirmación es completamente falsa?

Empecemos por el principio. ¿Qué es una espiral? En nuestro taller de “espirales”, destinado a alumnos de 4º de primaria, explicamos que una espiral se consigue combinando dos tipos de movimiento: uno circular alrededor de un punto, y uno lineal alejándose de dicho punto. De esta forma, una espiral es una línea curva generada por un punto que se va alejando progresivamente de un centro a la vez que gira alrededor de él. Con muchos ejemplos y varios métodos diferentes, los alumnos diferencian y dibujan espirales arquimedianas y logarítmicas.

Por otro lado, en nuestro taller “creciendo en proporción”, destinado a 1º de la ESO, hablamos de la sucesión de Fibonacci y del número áureo. Después de ver montones de ejemplos que aparecen por sí solos en la naturaleza, los alumnos quedan fascinados con la magia de este número. Una vez presentado el número áureo, mostramos los rectángulos áureos y, también, las espirales áureas.

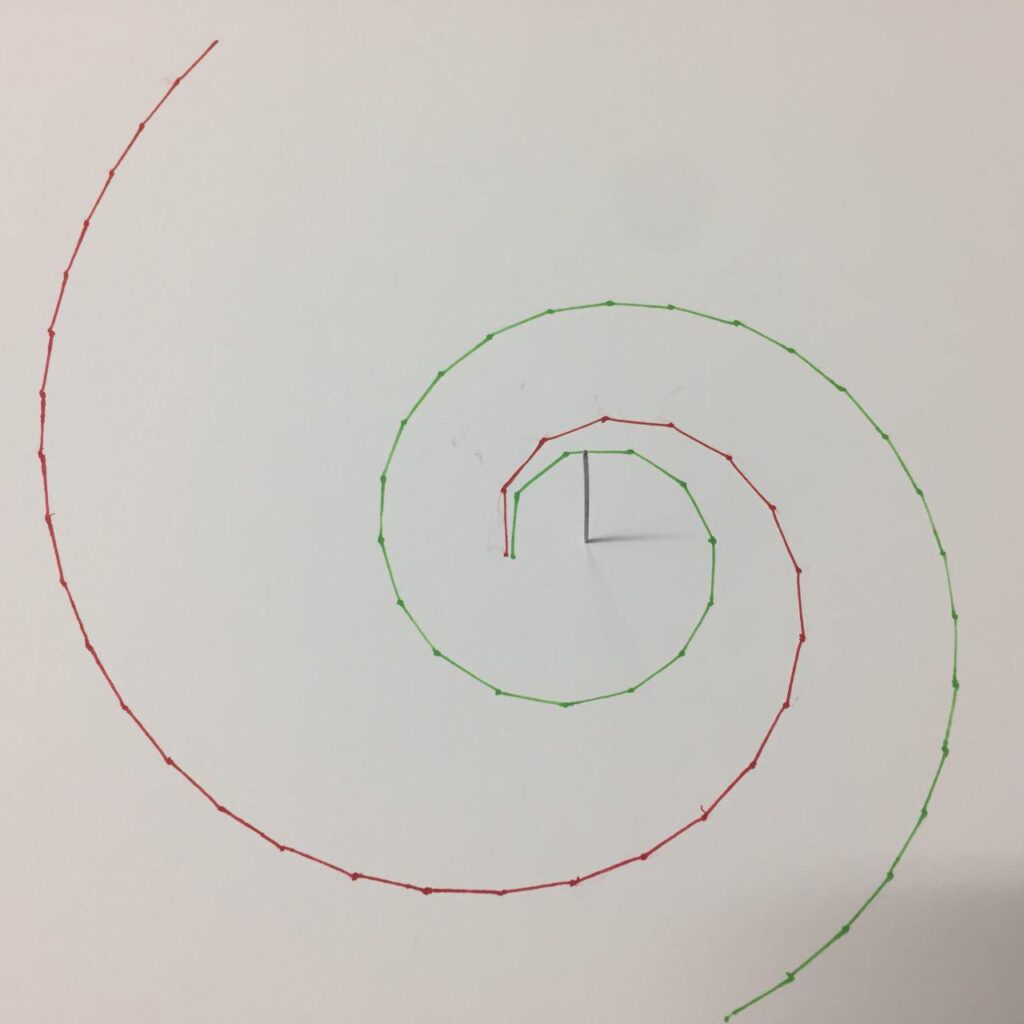
Aunque, como hemos dicho, en muchos libros y artículos relacionan la espiral dorada con la espiral del nautilus, si medimos con un calibre, o comparamos ambas espirales, vemos rápidamente que esta información es errónea. En la imagen puede verse cómo claramente ambas espirales no coinciden. Las dos espirales son logarítmicas y, además, están relacionadas con el número áureo, pero tienen diferente razón de crecimiento. Empiezan y terminan en el mismo punto pero el nautilus va abriéndose mucho más lentamente, es decir, da más vueltas hasta llegar al punto final.

Una regla que dibuja espirales

Basándonos en un método explicado por el gran Martin Gardner en su libro “El ahorcamiento inesperado y otros entretenimientos matemáticos”, en Divermates hemos querido enseñaros cómo construir una regla con la que podréis dibujar las dos espirales que queremos comparar y que tanta controversia han dado en el mundo de las matemáticas. En este libro Gardner nos enseña cómo fabricarnos una regla para construir espirales logarítmicas.

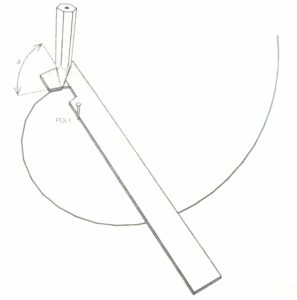
El ángulo a puede tomar cualquier valor entre 0º y 180º. Si escogemos exactamente un ángulo de 90º, estaremos dibujando una circunferencia, y si usamos un ángulo de 74º39′, la espiral resultante sería su propia envolvente. En nuestra regla hemos aprovechado los dos extremos para realizar dos espirales distintas. Justamente hemos seleccionado los ángulos que nos dibujarán las dos espirales a comparar: la espiral áurea y la espiral del nautilus.

Para construirte esta regla sólo necesitarás pegamento, tijeras, y las reglas que podrás descargarte aquí:

Regla para espirales (rectificada) DESCARGAR Enviar enlace de descarga a: Confirmo que he leído y acepto la condiciones de la Política de privacidad. Quiero recibir notificaciones de nuevos materiales gratuitos, actividades, sesiones de formación y divulgación de Divermates.

Recomendamos imprimir la regla en cartulina, para tener más rígidez. En cada copia vienen cuatro reglas. Lo primero que tienes que hacer es separar una de ellas, recortando el rectángulo por la línea más gruesa.

A continuación vamos a doblar por la línea de puntos y echar pegamento por la parte de atrás. Esto lo haremos para pegar doble capa de cartulina y así reforzar nuestra regla.

Por último, ya con la doble capa hecha, vamos a recortar la forma exacta de la regla.

¡Ya tienes tu regla! Sigue leyendo para entender cómo funciona.

¿Cómo funciona?

Lo primero que tenemos que hacer es marcar el polo de nuestra espiral. Una vez marcado vamos a mover la regla dejando el borde interno siempre sobre este polo. Lo más sencillo es clavar una aguja o un alfiler para apoyar la regla sobre él. A partir de aquí, iremos trazando pequeños segmentos apoyándonos en la recta oblicua mientras vamos girando nuestra regla en torno al polo, en dirección horaria o antihoraria. Es importante que al girar la regla siempre tengamos el borde interno situado tocando el polo. Además, tenemos que dibujar estos segmentos uniendo cada uno con el siguiente. El mecanismo asegura que todas estas cuerdas corten el radio vector formando el mismo ángulo. Es exactamente este hecho el que hace que la regla funcione, ya que al ser la espiral logarítmica una espiral equiangular, el ángulo entre el radio vector y la tangente es constante.

Al dibujar nuestra espiral con pequeños segmentos se produce un efecto que se asemeja mucho a la forma en que muchas arañas tejen su tela.

Espiral áurea y espiral del nautilus

Una vez que dibujadas ambas espirales puedes observar y comprobar sus diferencias.  En la imagen puedes ver en rojo la espiral áurea y en verde la espiral del nautilus.

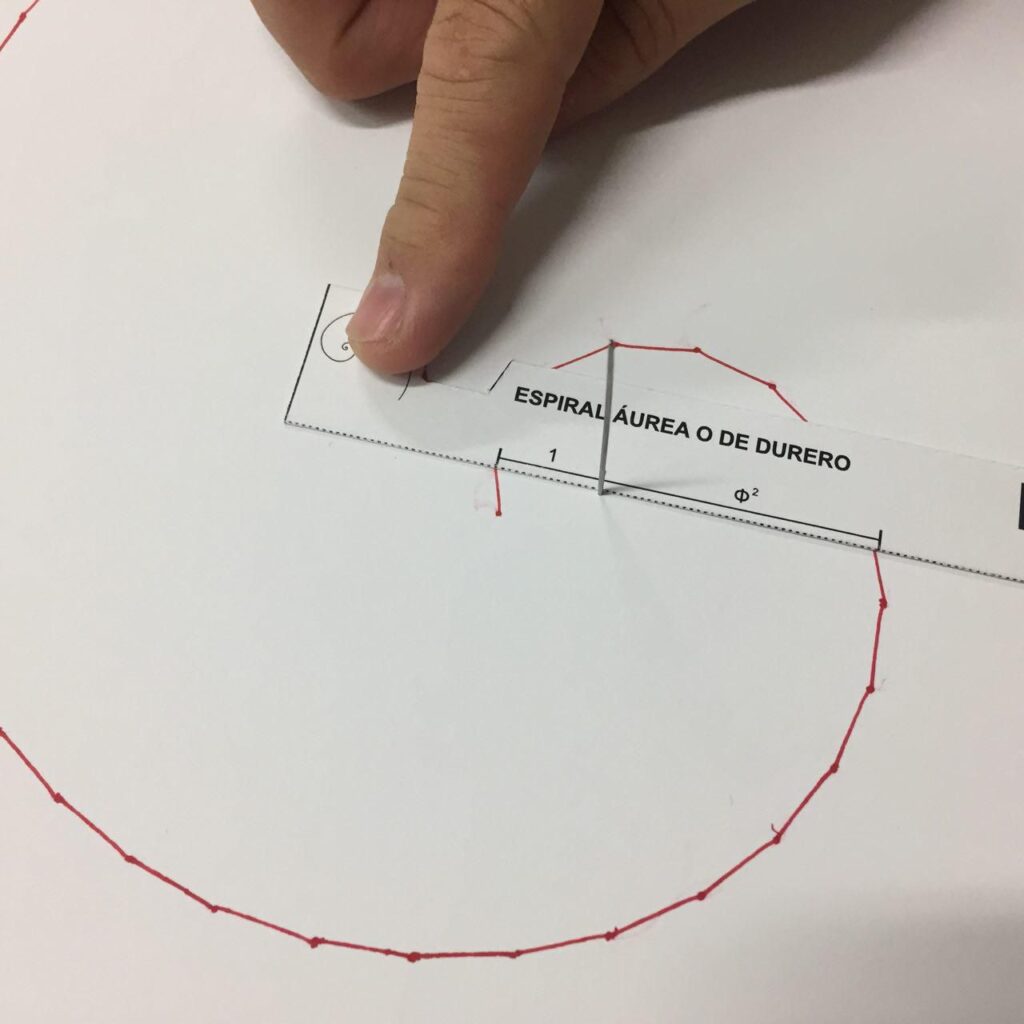
En el lado exterior de la regla hemos incluido, a cada lado, una cota con el crecimiento de ambas espirales. Podrás encontrar un punto en tu espiral donde, al poner el punto medio de la cota sobre el polo, las longitudes hasta las ramas de la espiral a cada lado coincidirán con las cotas. Como ves, ambas están relacionadas con el número de oro, una con phi y la otra con su cuadrado.

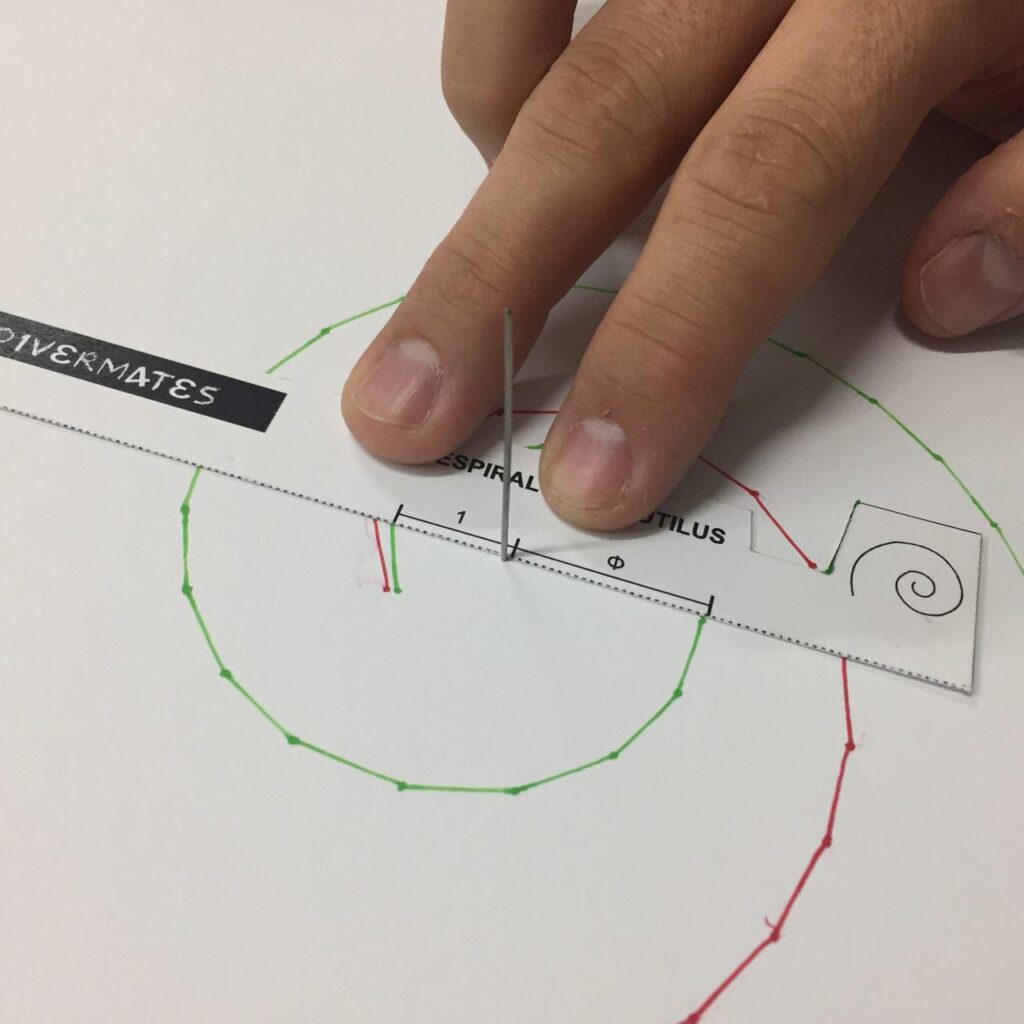
Al ser en la espiral del nautilus la proporción 1 al número de oro, si tenemos a mano un compás áureo podemos comprobar que esta proporción se cumple en todos los puntos de la espiral. Nosotros lo hemos comprobado con el compás áureo de Divermates.

¿Y entonces por qué se han relacionado siempre estas dos espirales como iguales?

No está muy claro. En el libro Estética de las proporciones en la naturaleza y en las artes, de Matila C. Ghyka, se habla de la relación del número de oro con el crecimiento de la concha de diferentes moluscos, pero distingue tres tipos de espirales.

• En la primera, la pulsación radial es el número de oro. Esta pulsación radial se refiere a la relación entre las distancias al dar una vuelta y la siguiente, en una misma dirección.

OC/OB=ϕ

• En la segunda, la pulsación diametral es el número de oro. Esta pulsación diametral se refiere a la relación entre las distancias a un punto y al punto diametralmente opuesto siguiente, situado a 180º. Justo esta espiral es la correspondiente al nautilus.

OD/OD´=ϕ

• En la última, la pulsación cuadrantral es el número de oro. Esta pulsación cuadrantal se refiere a la relación entre las distancias a un punto y al siguiente punto situado a 90º. Al tener pulsación cuadrantal ϕ, esta espiral tendrá pulsación diametral ϕ², por lo que es justo la espiral de Durero.

OD/OD´´=ϕ

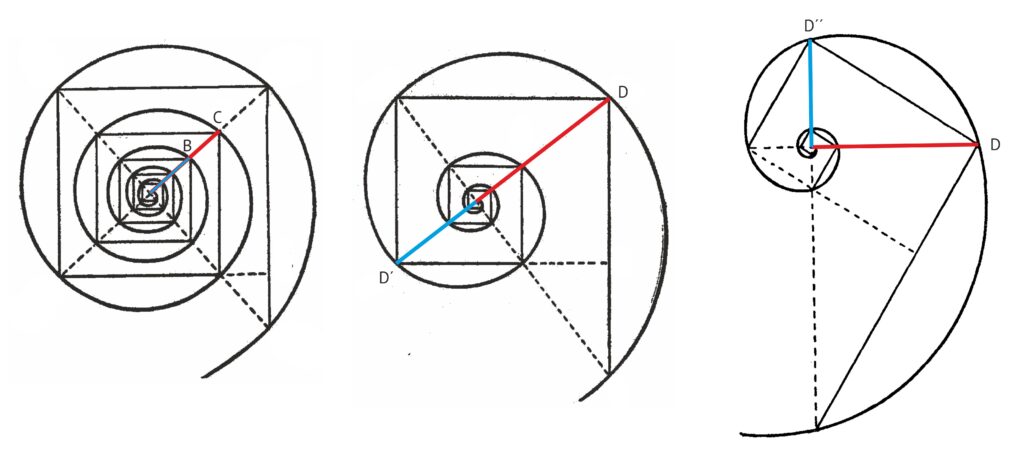
Posteriormente, en el cortometraje Donald en el país de las matemáticas, lanzado en 1959, el “señor Espíritu” enseña a Donald el número de oro y las proporciones áureas. Llega un momento en el que con la ayuda de la concha del nautilus, el Espíritu explica que las proporciones mágicas de la sección dorada son a menudo encontradas en las espirales de los diseños de la naturaleza. En realidad, lo que muestra en el fotograma de la imagen es que los segmentos naranjas, los verticales, están todos en proporción áurea. A partir de esos segmentos completa la espiral haciéndola coincidir con la espiral del nautilus. En realidad, las relaciones indicadas son correctas, pero desde Divermates creemos que ha podido dar lugar a que muchos espectadores relacionen directamente la espiral del molusco con la espiral áurea, aunque no sea correcta esta igualdad.

Como vemos, efectivamente la espiral del nautilus está relacionada con el número áureo. Dicha relación ha podido llegar, con el paso de los años, de libro en libro y artículo en artículo, a relacionar, erróneamente, la espiral del nautilus con la espiral áurea.

En cualquier caso, esta falsa relación nos parece un buen ejemplo con el que enseñar a los más jóvenes que las matemáticas, y la ciencia en general, deben buscar el pensamiento crítico, y que se debe cuestinar y comprobar todo, incluso lo que muchas veces damos por cierto solo por haberlo leído en muchos libros o páginas web.

Notas

Lo más importante de la ciencia es que todos nos revisamos continuamente para ser lo más rigurosos posibles. Ante la publicación de nuestra entrada sobre la espiral áurea y la del Nautilus hemos recibido un comentario de José R. Galo Sánchez señalando que nuestra aproximación no es la más ajustada. A pesar de recogerse en alguna bibliografía (Fletcher, R. (Feb 1988). Proportion and the Living World. Parabola,13 (1)), parece ser que la pulsación diametral 1:phi que incluimos en nuestro artículo no es la mejor aproximación a la espiral de la concha del Nautilus. Como José R. Galo Sánchez indica en su artículo (Galo Sánchez, J.R., Cabezudo Bueno, Á., y Fernández Trujillo, I. (2016). Sobre la forma y el crecimiento cordobés del Nautilus Pompilius. Épsilon, 33 (94),81-110.) el factor de crecimiento del Nautilus es 3 o próximo a 3 (lo que supondría una pulsación cuadrantal r=1,31607), por lo que realmente la espiral cordobesa se ajustaría con mucha más precisión (pulsación cuadrantal 1,3065 frente nuestra pulsación cuadrantal sqrt(phi)=1,2720).

Puedes descargarte una nueva regla que hemos diseñado donde podrás comparar estas dos espirales:

BIBLIOGRAFIA

Gardner, M. (2018), El ahorcamiento inesperado y otros entretenimientos matemáticos, Madrid, Alianza Editorial

Ghyka, M. (1946), The geometry of Art and Life, Dover Publications